単振動

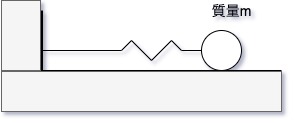
水平方向の運動方程式を立てる。 力を図示すると以下のようになる。

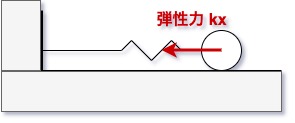
\begin{eqnarray} m a & = & F \newline & = & - k x \newline (k& : &バネ定数) \end{eqnarray}

単振動の周期は一般的に

\begin{eqnarray} 周期　T & = & 2 \pi \sqrt{ \frac{m}{k} } \newline 角振動数　\omega & = & \frac{2 \pi}{T} = \sqrt{ \frac{k}{m} } \end{eqnarray} と書くことができる

$x$の一般解について \begin{eqnarray} x & = & A sin(\omega t + \alpha ) \newline (\omega&:& 角振動数, \alpha: 位相) \end{eqnarray}

である。